標準誤差(SE)とは一般的な概念なので、その中から特に「平均値」についての標準誤差について触れようと思います。医学の分野や生物学の分野などの文献に平均値(Mean)とともによく見られる統計量です。しかし、標準偏差と標準誤差を混同しているケースが多いように思います。
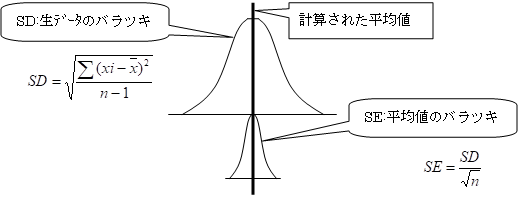
標準偏差は集められた測定値のばらつき具合を表すのに対して、標準誤差は求められた平均値のばらつきを表しています。
計算は次の式で行われます。
SE=SD/√N
N:測定回数
SE:標準誤差
SD:標準偏差
実際の例で考えてみましょう。
例えば:
A群(Mean=100、SD=10、N=16)、
B群(Mean=100、SD=10、N=10000)の2群の測定値があったとします。
平均値、標準偏差ともに同じで測定回数のみ異なります。
さて、どちらの群の平均値が信頼性が高いでしょうか?
経験的にも回数が多いB群が信頼性が高いだろと考えられます。
そこでその指標になる標準誤差を計算してみることにします。
A群(Mean =100、SD=10、N=16 → SE=10/√16 =2.5)、
B群(Mean =100、SD=10、N=10000 → SE=10/√10000=0.1)となります。
さらに得られた標本から考えられる本当の値(真の平均値(μ))は、標本から求められた平均値の信頼区間にその確率で含まれており、次の式で計算できます。
μ=M±t×SD/√N
t:N-1(自由度φ)と信頼レベル(有意水準α)に基づくt分布表より導かれます。
それ等を用いて、各群の平均値の信頼性を求めてみると、
A群では、自由度φ=N-1=15、有意水準α=0.05とすると t値=2.131となります。
そこから求める信頼区間は,94.7 から 105.3となります。その幅は、10.7となります。
また、B群では(自由度φ=N-1=99、有意水準α=0.05とすると t値=1.984となります。そこから求める信頼区間は 99.8から100.2となりその幅は0.4となります。
それより明らかにB群の信頼性が高いことになるわけです。
同じ標準偏差なら回数が多くなれば信頼性が高くなります。そして同じ回数なら標準偏差が小さいほど信頼性が高いことになるわけです。
臨床の場面では、各疾患群の薬効やステージによって得られた代表値である平均値を用いて判断をくだす場合が多いわけです。そのため平均値の信頼性のものさしである標準誤差が多く用いられるわけです。まさしく平均値の差の検定はこの標準誤差が判断の物差しとなっています。
臨床検査での標準化に欠かせない正確さの評価法でのかたよりの計算にもこの標準誤差が用いられています。
標準誤差と標準偏差を間違いないようにいたしましょう。
参考資料・文献
1)臨床化学における定量検査の精密さ・正確さ評価法指針(改訂版)(GC-JAMT1-1999),日本臨床検査標準協議会会誌、51、3‐26、1999
2)井野邦英,臨床検査統計学講座Ⅰ,全国社会保険技師会会誌,1999
3)井野邦英,データのまとめ方と考え方 第10版,2015
文責:井野邦英 アキュプレック